Тема 3.4: Зубчасті передачі.
План
1. Призначення, будова, принцип роботи, застосування зубчастих передач. Класифікація зубчастих передач. Підрізання та коригування зубів. Точність зубчастих передач. Основні вимоги до зубчастого зчеплення.
2. Матеріали і конструкції зубчастих коліс.
3. Види руйнування зубів.
4. Прямозубі циліндричні передачі. Основні геометричні співвідношення. Сили, що діють у зачепленні.
5. Розрахунок зубів на контактну і згинальну витривалість. Вибір основних параметрів, розрахункових коефіцієнтів, допустимих напружень.
6. Непрямозубі циліндричні передачі. Основні геометричні співвідношення. Сили, що діють у зачепленні.
7. Особливості розрахунку непрямозубих передач на контактну міцність та згин.
8. Прямозубі конічні передачі: основні геометричні співвідношення.
9. Сили в зачепленні.
10. Особливості розрахунку, конструкція зубчастих коліс.

1. Призначення, будова, принцип роботи, застосування зубчастих передач. Класифікація зубчастих передач. Підрізання та коригування зубів.
Зубчаста циліндрична передача – це трьохланковий механізм у якого дві рухомі ланки є
циліндричними зубчастими колесами (рис. 4.1). Менше з двох зубчастих коліс 1
називається шестернею,
а більше 2 – колесом. Термін “зубчасте колесо” належить до обох коліс передачі.
Розміри зубчастих коліс можуть вимірюватись кількома міліметрами (у приладах),
а в найпотужніших машинах до 10 м. Зубчасті циліндричні
передачі здатні передавати потужність до десятків тисяч кВт при
швидкості до 150 м/c і більше з коефіцієнтом корисної дії рівним
0,94...0,99. Оптимальне передаточне число ![]() .
.
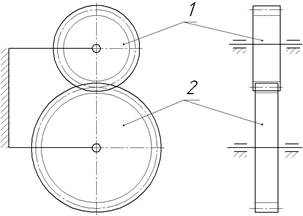
Рис.4.1. Схема зубчастої циліндричної передачі
Зубчасті циліндричні передачі класифікують за такими ознаками:
- за формою поперечного перетину зубців: евольвентні (рис. 4.2, а);
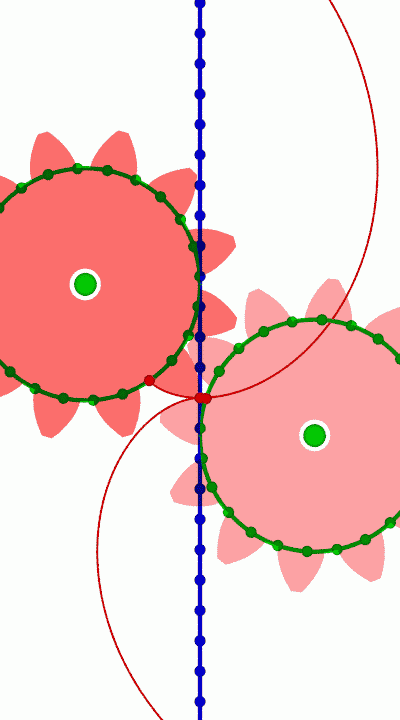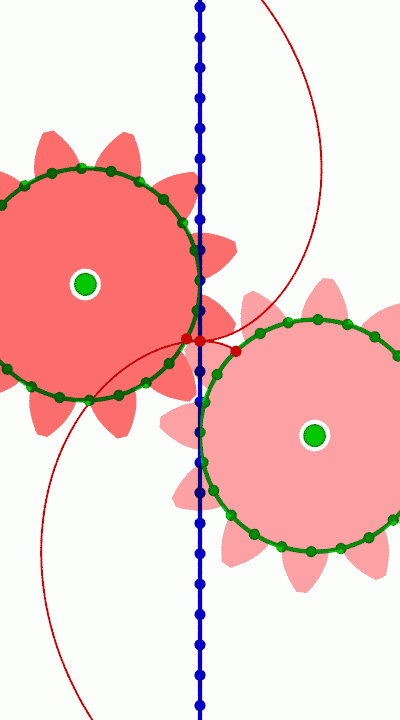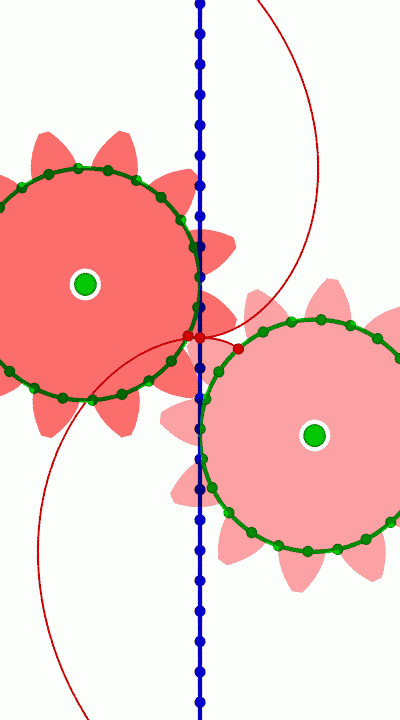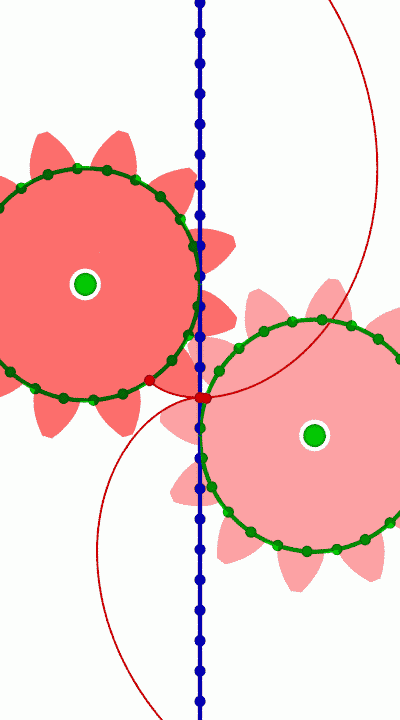
циклоїдні (рис. 4.2, б);

кругові (зачеплення Новікова) (рис. 4.2, в);

Рис. 4.2. Схеми форм поперечного перетину зуба
- за розміщенням на зубчастому вінці зубців:
прямозубі (рис. 4.3, а);

косозубі (рис. 4.3, б);

шевронні (рис. 4.3, в);

кругові ( рис. 4.3, г);

аркові (рис. 4.3, д);

Рис. 4.3. Схеми розміщення на зубчастому вінці зубців
- за відносним розміщенням зубчастих коліс:
зовнішнього зачеплення (рис. 4.4, а);

внутрішнього зачеплення (рис. 4.4, б);

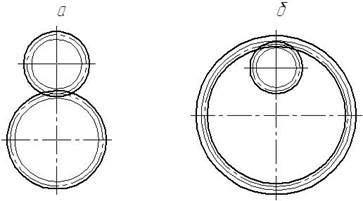
Рис. 4.4. Схеми відносного розміщення зубчастих коліс
- за конструкцією корпуса:
відкриті (рис. 4.5, а);

закриті (рис. 4.5, б).

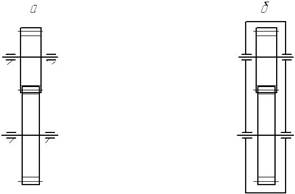
Рис. 4.5. Схеми передач за конструкцією корпуса
Виготовлення зубчастих коліс. Заготовки зубчастих коліс отримують литтям, ковкою або різанням. Зуби коліс виготовляють накатуванням, нарізанням, рідше литтям.
Накатування зубів. Застосовується в масовому виробництві. Попереднє формоутворення зубів циліндричних і конічних коліс проводиться гарячим накатуванням. Вінець стальної заготовки нагрівають токами високої частоти до температури ~ 1200ºС, а потім обкатують між колесами-обкатниками. При цьому на вінці видавлюються зуби. Для отримання коліс більш високої точності проводять послідуючу механічну обробку зубів або холодне накатування – калібрування.
Холодне накатування зубів застосовують при модулі до 1 мм.
Нарізання зубів. Існує два методи нарізання зубів: копіювання і обкатка. Метод копіювання заключається в прорізанні впадин між зубами модульними фрезами: дисковими або пальцевими. Після прорізання впадини заготовку повертають на крок зачеплення. Профіль впадини представляє собою копію профілю ріжучої кромки фрези. Метод копіювання – неточний, використовується в основному в ремонтному ділі.
Нарізання зубів методом обкатки оснований на відтворенні зачеплення зубчастої пари, одним з елементів якої є ріжучий інструмент – черв’ячна фреза, довбяк або реєчний довбяк – гребінка. Черв’ячна фреза має в осьовому січенні форму інструментальної рейки. При нарізанні зубів заготовка і фреза обертаються навколо своїх осей, забезпечуючи безперервність процесу.
Нарізання зубів черв’ячними фрезами широко використовують для виготовлення циліндричних коліс з зовнішнім розміщенням зубів. Для нарізання коліс з внутрішнім розміщенням зубів застосовують довбяки. Гребінками нарізають прямозубі і косозубі колеса з великим модулем зачеплення.
Нарізання зубів конічних коліс методом обкатки проводять струганням, фрезеруванням, інструментом з прямобічним профілем або різцевими головками.
Зуби точних коліс після нарізання підлягають обробці шевінгуванням, шліфуванням, притиркою або обкаткою.
Шевінгування застосовують для тонкої обробки незагартованих коліс. Виконують інструментом – шевером, який має вид зубчастого колеса з вузькими канавками на поверхні зубів. Обертаючись в зачепленні колесом, шевер знімає ріжучими кромками канавок волосоподібні стружки з зубів колеса.
Шліфування використовують для обробки загартованих зубів. Виконують шліфувальними кругами способом копіювання або обкатки.
Притирку виконують для обробки загартованих зубів. Виконують притиром – чавунним, точно виготовленим колесом з використанням притирочних абразивних паст.
Обкатка застосовується для загладжування шорсткості на поверхні незагартованих коліс. На протязі 1-2 хв. зубчате колесо обкатують під навантаженням з еталонним колесом великої твердості.
Поняття про зубчасте зачеплення зі зміщенням.
Корегуванням називається покращення профіля зуба шляхом його окреслення другою ділянкою тієї ж самої евольвенти порівняно з нормальним зачепленням.
Корегування застосовується:
а ) для усунення підрізання зубів шестерні при z<zmin;
б ) для підвищення згінної міцності зубів, що досягається збільшенням їх товщини;
в ) для підвищення контактної міцності, що досягається збільшенням радіусу кривизни в полюсі зачеплення;
г ) для одержання заданої міжосьової відстані.
Корегування здійснюється зміщенням інструментальної рейки на величину xm. Додатним називається зміщення рейки від центра колеса, від’ємним – до центру.
Точність зубчастих передач.
При виготовленні зубчастих передач виникають похибки, які виражаються в відхиленнях кроку, співосності коліс, теоретичного профілю зубів, міжосьової відстані та ін. Всі ці похибки приводять до збільшеного шуму під час роботи та передчасному зносу передачі.
Точність зубчастих передач регламентується стандартами, в яких передбачено 12 степенів точності з позначенням степенів в порядку зменшення точності. Найбільше розповсюдження мають 6, 7, 8, 9-а степені точності. 6 степінь – високоточні передачі, 9 – тихохідні передачі пониженої точності.
2. Матеріали і конструкції зубчастих коліс.
Виготовляють
зубчасті колеса із різноманітних матеріалів. Основним із них є сталь. Найбільше
застосування мають якісні конструкційні сталі 40, 45, 50, сталі з підвищеним
вмістом марганцю 40Г2, 50Г, леговані
сталі 40Х, 40ХН, 40ХНМА, 35ХГСА, сталеве литво – сталі 40Л, 45Л, 50Л, сірі
чавуни марок СЧ18 – СЧ35 та інші. Сталі допускають зміну твердості і міцності
за рахунок термічної або хіміко-термічної обробки, якою є нормалізація,
поліпшення, об’ємне і поверхневе гартування,
цементація
та азотування.
Залежно від твердості після термообробки сталеві зубчасті колеса поділяють на
дві групи: з твердістю ![]() (нормалізація і поліпшення)
і з твердістю
(нормалізація і поліпшення)
і з твердістю ![]() (об’ємне і поверхневе
гартування, цементація та азотування). Твердість шестірні
(об’ємне і поверхневе
гартування, цементація та азотування). Твердість шестірні ![]() рекомендують назначати більшою
від твердості колеса
рекомендують назначати більшою
від твердості колеса ![]() (
(![]() ). Зубчасті колеса з твердістю
). Зубчасті колеса з твердістю ![]() нарізають
після термообробки заготовки, а з твердістю
нарізають
після термообробки заготовки, а з твердістю ![]() до термообробки.
Тому термообробку здійснюють після нарізування зубців.
до термообробки.
Тому термообробку здійснюють після нарізування зубців.
3. Види руйнування зубів.
Практика експлуатації зубчастих передач показує, що найбільш характерними є такі види руйнування зубців: втомне викришування активних поверхонь (рис. 4.6, а), поломка зубців (рис. 4.6, б), відшарування поверхневих шарів зубців(рис. 4.6, в), абразивне спрацювання(рис. 4.6, г), пластична деформація(рис. 4.6, д) та заїдання зубців(рис. 4.6, е).
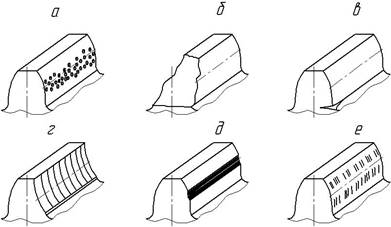
Рис. 4.6. Види руйнування зубців зубчастих коліс
Основними
критеріями роботоздатності зубців зубчастих коліс є
міцність та зносостійкість. Найглибше теоретично і практично досліджені явища
втомного викришування активних поверхонь зубців, що спричинені
контактними напруженнями ![]() ,
та явища поломки зубців, які є результатом циклічної дії напружень згину
,
та явища поломки зубців, які є результатом циклічної дії напружень згину ![]() . Вибір норм допустимих напружень
. Вибір норм допустимих напружень ![]() та
та ![]() сприяє запобіганню появи інших
наведених видів руйнування зубців зубчастих коліс.
сприяє запобіганню появи інших
наведених видів руйнування зубців зубчастих коліс.
Допустимі напруження.
Допустимі контактні напруження (тут і далі при розрахунках зубчастих передач уведені деякі спрощення щодо ГОСТ 21354-87):
![]() (4.1)
(4.1)
де ![]() - межа
контактної витривалості поверхневих шарів зубців, яка відповідає базі
випробувань
- межа
контактної витривалості поверхневих шарів зубців, яка відповідає базі
випробувань ![]() Для
матеріалів з
Для
матеріалів з ![]()
![]() а
а
![]() ;
(4.2)
;
(4.2)
![]() - коефіцієнт
безпеки, який враховує ступінь відповідальності передачі. Для передач
загального призначення, при однорідній по об’єму структурі матеріалу, яка
забезпечується термообробкою нормалізацією або поліпшенням -
- коефіцієнт
безпеки, який враховує ступінь відповідальності передачі. Для передач
загального призначення, при однорідній по об’єму структурі матеріалу, яка
забезпечується термообробкою нормалізацією або поліпшенням - ![]() . При неоднорідній структурі
(поверхневе гартування, цементація, азотування) -
. При неоднорідній структурі
(поверхневе гартування, цементація, азотування) - ![]() ;
; ![]() - коефіцієнт довговічності. Враховує
вплив строку служби і режиму навантаження передачі. Визначається з
співвідношення
- коефіцієнт довговічності. Враховує
вплив строку служби і режиму навантаження передачі. Визначається з
співвідношення ![]() і
і
![]() Сумарне число
циклів навантаження зубців за весь строк роботи передачі знаходиться за
формулою
Сумарне число
циклів навантаження зубців за весь строк роботи передачі знаходиться за
формулою
![]() (4.3)
(4.3)
Тут: ![]() - строк
служби передачі в годинах;
- строк
служби передачі в годинах; ![]() -
кутова швидкість шестерні (
-
кутова швидкість шестерні (![]() )
або колеса (
)
або колеса (![]() ),
), ![]() .
.
Для довгопрацюючих передач при ![]() , коефіцієнт довговічності
приймається:
, коефіцієнт довговічності
приймається:
- при змінних режимах
навантаження ![]() ;
;
- при постійних режимах навантаження визначається за формулою
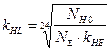 ,
але
,
але ![]() 0,9.
(4.4)
0,9.
(4.4)
При ![]() для
змінного і постійного режимів навантаження
для
змінного і постійного режимів навантаження
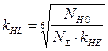 ,
але
,
але ![]() 2,6.
(4.5)
2,6.
(4.5)
Тут ![]() -
коефіцієнт інтенсивності навантаження.
-
коефіцієнт інтенсивності навантаження.
Допустимі контактні напруження визначаються для шестерні (![]() ) і для колеса (
) і для колеса (![]() ). Для розрахунку передачі
приймається менше із двох допустимих напружень.
). Для розрахунку передачі
приймається менше із двох допустимих напружень.
Допустимі напруження при згині
![]() (4.6)
(4.6)
де ![]() - межа
витривалості зубців при згині, яка відповідає базі випробувань
- межа
витривалості зубців при згині, яка відповідає базі випробувань ![]() Для матеріалів з
Для матеріалів з ![]()
![]() а
а
![]() ;
(4.7)
;
(4.7)
![]() - коефіцієнт
довговічності: при
- коефіцієнт
довговічності: при ![]() приймається
приймається
![]() , при
, при ![]() визначається за формулою
визначається за формулою
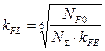 ,
але
,
але ![]() 2,0,
(4.8)
2,0,
(4.8)
де ![]() -
коефіцієнт інтенсивності режиму навантаження;
-
коефіцієнт інтенсивності режиму навантаження;
![]() - коефіцієнт
реверсивності навантаження;
- коефіцієнт
реверсивності навантаження; ![]() -
коефіцієнт безпеки.
-
коефіцієнт безпеки.
Всі коефіцієнти вибираються із довідкової літератури. Допустимі
напруження при згині визначають для шестерні (![]() ) і для колеса (
) і для колеса (![]() ).
).
Рекомендації щодо граничних контактних напружень ![]() і граничних напружень згину
і граничних напружень згину ![]() наведені в літературі з деталей
машин.
наведені в літературі з деталей
машин.
4. Прямозубі циліндричні передачі. Основні геометричні співвідношення. Сили, що діють у зачепленні.

В прямозубій передачі зуби входять в зачеплення зразу по всій довжині. Через неточність виготовлення передачі і її зносу процес виходу однієї пари зубів із зачеплення і початок зачеплення іншої пари супроводжується ударами і шумом, сила яких зростає із збільшенням колової швидкості коліс. Прямозубі передачі використовують при невисоких та середніх колових швидкостях; відкриті передачі, як правило, роблять прямозубими.
Згідно основної теореми зачеплення для понижуючих передач передаточне число u = ω1/ ω2 = d2/d1 = z2/z1. Для пари циліндричних зубчатих коліс рекомендується u<3...6.

Рис. 4.7. Геометричні розміри циліндричної зубчастої передачі
Розміри зубчатого колеса виражають через модуль і число зубів z.
Ділильний і початковий діаметри d = dω = mz
Діаметр вершин da = d + 2ha = d + 2m
Діаметр впадин df = d – 2hf = d – 2,5m
![]()
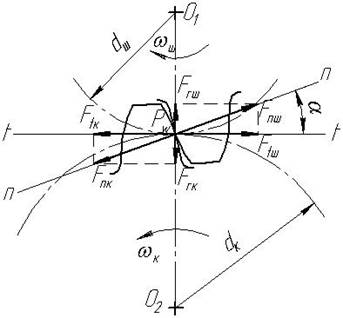
Рис. 4.8. Схема сил у зачепленні
В прямозубих циліндричних передачах ( рис. 4.8 і рис. 4.9, а):
- колова сила ![]() ;
;
- радіальна сила ![]() ;
(4.18)
;
(4.18)
- осьова сила ![]() .
.
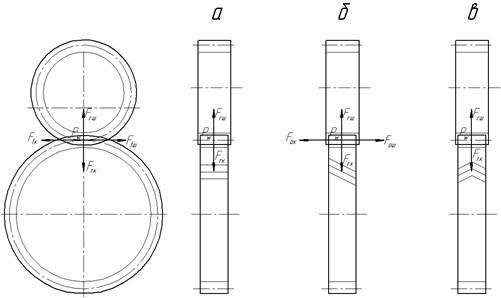
Рис. 4.9. Схема сил у передачах
5. Розрахунок зубів на контактну і згинальну витривалість. Вибір основних параметрів, розрахункових коефіцієнтів, допустимих напружень.
Загальні відомості про розрахунок на міцність циліндричних
евольвентних зубчастих передач
Розрахунком на міцність визначають розміри зубчастої передачі, при яких не виникає небезпека пошкодження зубів коліс. Це можливо при взаємозв’язаному розрахунку міцності та геометрії зачеплення, тому що із зміною геометрії міняється і навантажувальна спроможність зубчастого зачеплення.
Розрахунок на міцність сталевих циліндричних зубчастих передач зовнішнього зачеплення з модулем m > 1 мм стандартизований. В курсі “Деталі машин” вивчають основи такого розрахунку. При цьому вводять деякі спрощення, які мало впливають на результати для більшості випадків практики. В розрахунках використовують багато різних коефіцієнтів. Коефіцієнти, загальні для розрахунку на контактну міцність та згин, позначають буквою К, спеціальні коефіцієнти для розрахунку на контактну міцність - буквою Z, на згин – буквою Y.
Закриті передачі розраховують на попередження викришування робочих поверхонь зубів і їх поламки (згину). Розміри передачі визначають розрахунком на контактну міцність, а розрахунок зубів несе перевірочний характер з ціллю визначення мінімально можливого значення модуля.
Відкриті зубчасті передачі розраховують на контактну міцність з послідуючою перевіркою зубів на згин з розрахунком їх зносу.
Розрахунок прямозубих передач на втому і міцність при згині.
При розрахунках на втому при згині зубець розглядається як консольна балка (рис. 4.10). Розрахункове навантаження прикладається до вершини зубця, тобто коли він входить у зачеплення. Це найнебезпечніший випадок навантаження зубця, при якому виникають максимальні напруження згину у його основі.
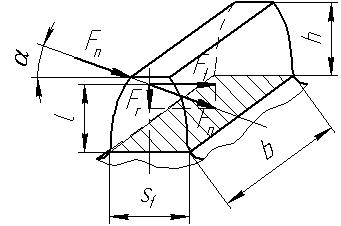
Рис. 4.10. Розрахункова схема зуба на згин
Перенесемо точку прикладання сили ![]() на
вісь симетрії зубця і розкладемо на сили
на
вісь симетрії зубця і розкладемо на сили ![]() і
і
![]() . Сила
. Сила ![]() згинає, а сила
згинає, а сила ![]() - стискає зубець. Деформація стиску
незначна і ми нехтуємо нею. Запишемо умову міцності
на згин
- стискає зубець. Деформація стиску
незначна і ми нехтуємо нею. Запишемо умову міцності
на згин
![]() ,
(4.19)
,
(4.19)
де ![]() - момент згину;
- момент згину; ![]() - момент опору згину основи
зубця. Розміри
- момент опору згину основи
зубця. Розміри ![]() ,
,
![]() і
і ![]() показані на рис. 4.10.
Величини
показані на рис. 4.10.
Величини ![]() і
і
![]() пропорціональні
модулю
пропорціональні
модулю ![]() :
: ![]() , а
, а ![]() , де
, де ![]() і
і ![]() - коефіцієнти
пропорціональності. Підставимо значення
- коефіцієнти
пропорціональності. Підставимо значення ![]() і
і ![]() в умову міцності на згин,
отримаємо:
в умову міцності на згин,
отримаємо:
![]() ,
(4.20)
,
(4.20)
де ![]() - коефіцієнт форми зубця, який
залежить від числа зубців шестерні (
- коефіцієнт форми зубця, який
залежить від числа зубців шестерні (![]() )
або колеса (
)
або колеса (![]() ). На
рис. 4. 11 показані схеми форм зубців: на рис. 4. 11, а - для
зубчастого колеса з
). На
рис. 4. 11 показані схеми форм зубців: на рис. 4. 11, а - для
зубчастого колеса з ![]() ,
де профіль зуба складається з евольвенти 1, радіальної ділянки 2 і галтелі 3;
рис. 4. 11, б - для зубчастого колеса з
,
де профіль зуба складається з евольвенти 1, радіальної ділянки 2 і галтелі 3;
рис. 4. 11, б - для зубчастого колеса з ![]() , де профіль зуба складається з
евольвенти 1 і галтелі 3.
, де профіль зуба складається з
евольвенти 1 і галтелі 3.
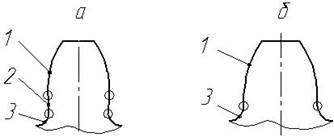
Рис.4.11. Схеми форм зубців
Якщо виразити колову силу ![]() через
крутний момент
через
крутний момент ![]()
![]() .
(4.21)
.
(4.21)
При перевірочних розрахунках оцінюється втомна міцність зуба шестерні та зуба колеса.
При проектному розрахунку приймають ![]() і
визначають модуль
і
визначають модуль
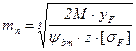 ,
(4.22)
,
(4.22)
де ![]() - коефіцієнт ширини зубчастого
вінця.
- коефіцієнт ширини зубчастого
вінця.
Отримане значення ![]() округляється
до стандартного. Такий проектний розрахунок виконується для відкритих зубчастих
передач.
округляється
до стандартного. Такий проектний розрахунок виконується для відкритих зубчастих
передач.
Щоб забезпечувати потрібну міцність зубців при згині максимальним навантаженням, необхідно виконувати таку умову:
![]() .
(4.23)
.
(4.23)
Розрахунок прямозубих передач на контактну втому та міцність.
У цьому прикладі розглядається зубчаста циліндрична прямозуба передача з
зовнішнім зачепленням зубців. Розрахунок активних поверхонь зубців на контактну
втому ведеться для моменту зачеплення їх у полюсі ![]() , оскільки викришування починається в
зоні полюсної лінії (рис. 4.12).
, оскільки викришування починається в
зоні полюсної лінії (рис. 4.12).
Запишемо умову контактної міцності
![]() ,
(4.24)
,
(4.24)
де ![]() - розподілене навантаження в
контакті зубців. Якщо
- розподілене навантаження в
контакті зубців. Якщо![]() ,
а
,
а ![]() , тоді
, тоді ![]() ;
; ![]() - зведений модуль пружності
першого роду, де
- зведений модуль пружності
першого роду, де ![]() -
модулі пружності першого роду, відповідно матеріалів шестерні і колеса;
-
модулі пружності першого роду, відповідно матеріалів шестерні і колеса; ![]() - зведений радіус кривини
евольвент у точці
- зведений радіус кривини
евольвент у точці ![]() контакту
зубців. Зведена кривина евольвент у точці контакту
контакту
зубців. Зведена кривина евольвент у точці контакту
![]() ,
(4.25)
,
(4.25)
де ![]() - радіус кривини евольвенти
зуба шестерні;
- радіус кривини евольвенти
зуба шестерні; ![]() -
радіус кривини евольвенти зуба колеса.
-
радіус кривини евольвенти зуба колеса.
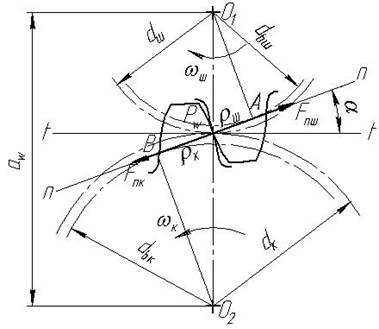
![]()
Рис. 4.12. Розрахункова схема на контактну деформацію
Якщо ![]() , після
підстановки отримаємо
, після
підстановки отримаємо
![]() .
(4.26)
.
(4.26)
Підставимо значення ![]() і
і
![]() в умову
контактної міцності , після перетворень отримаємо:
в умову
контактної міцності , після перетворень отримаємо:
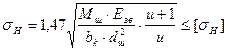 .
(4.27)
.
(4.27)
Отримана умова міцності контакту зубців при перевірочному розрахунку. При
проектному розрахунку визначається міжосьова відстань ![]() . Якщо прийняти, що
. Якщо прийняти, що ![]() , а
, а ![]() і підставити в умову міцності,
після перетворень отримаємо:
і підставити в умову міцності,
після перетворень отримаємо:
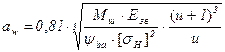 .
(4.28)
.
(4.28)
Далі визначають модуль зачеплення ![]() , округляють до стандартного значення
і розраховують геометричні розміри закритих циліндричних прямозубих передач.
, округляють до стандартного значення
і розраховують геометричні розміри закритих циліндричних прямозубих передач.
Щоб забезпечувати потрібну контактну міцність зубців при максимальному навантаженні, необхідно виконувати таку умову:
![]() .
(4.29)
.
(4.29)
6. Непрямозубі циліндричні передачі. Основні геометричні співвідношення. Сили, що діють у зачепленні.

Основний геометричний параметр зубчастої непрямозубої
циліндричної передачі є модуль ![]() - число міліметрів діаметра (
- число міліметрів діаметра (![]() ) ділильного кола, що припадає на
один зуб (
) ділильного кола, що припадає на
один зуб (![]() ). Зубчасті
циліндричні передачі мають два модулі:
). Зубчасті
циліндричні передачі мають два модулі: ![]() -
нормальний і
-
нормальний і ![]() – торцевий.
Стандартним є нормальний модуль. Зв’язок між модулями має вид:
– торцевий.
Стандартним є нормальний модуль. Зв’язок між модулями має вид: ![]() , де
, де ![]() - кут нахилу зубців,
приймається: для косозубих коліс
- кут нахилу зубців,
приймається: для косозубих коліс ![]() ; для шевронних коліс
; для шевронних коліс![]() .
.
Для визначення
геометричних розмірів зубчастої циліндричної передачі потрібно мати число
зубців шестерні (![]() ) і число
зубців колеса (
) і число
зубців колеса (![]() ).
Рекомендується приймати
).
Рекомендується приймати ![]() ,
а
,
а ![]() , де
, де ![]() - передаточне число зубчастої
циліндричної передачі.
- передаточне число зубчастої
циліндричної передачі.
В косозубих циліндричних передачах (рис. 4.9, б):
- колова сила ![]() ;
;
- радіальна сила ![]() ;
(4.30)
;
(4.30)
- осьова сила ![]() .
.
В шевронних циліндричних передачах (рис. 4.9, в):
- колова сила ![]() ;
;
- радіальна сила
![]() ;
(4.31)
;
(4.31)
- осьова сила ![]() .
.
7. Особливості розрахунку непрямозубих передач на контактну міцність та згин.
В інженерній практиці використовуються загальні вирази для розрахунків прямозубих, косозубих і шевронних передач.
При розрахунках на втому при згині:
- перевірочний розрахунок
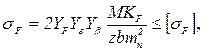 (4.32)
(4.32)
де ![]() - коефіцієнт форми зуба: вибирається
за еквівалентним числом зубців шестерні (
- коефіцієнт форми зуба: вибирається
за еквівалентним числом зубців шестерні (![]() )
і колеса (
)
і колеса (![]() ):для
прямозубих передач
):для
прямозубих передач ![]() і
і
![]() ; для косозубих і шевронних передач
; для косозубих і шевронних передач ![]() і
і ![]() ;
; ![]() - коефіцієнт перекриття зубців;
- коефіцієнт перекриття зубців;
![]() - коефіцієнт
нахилу зубів: визначається
- коефіцієнт
нахилу зубів: визначається ![]() .
Тут кут
.
Тут кут ![]() в градусах;
в градусах; ![]() - коефіцієнт навантаження при згині,
визначається за формулою
- коефіцієнт навантаження при згині,
визначається за формулою ![]() ,
де
,
де ![]() - коефіцієнт
розподілу навантаження між зубцями;
- коефіцієнт
розподілу навантаження між зубцями; ![]() -
коефіцієнт розподілу навантаження по ширині вінця зубчастого колеса;
-
коефіцієнт розподілу навантаження по ширині вінця зубчастого колеса; ![]() - коефіцієнт динамічності
навантаження.
- коефіцієнт динамічності
навантаження.
- проектний розрахунок
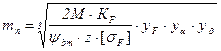 .
(4.33)
.
(4.33)
При розрахунках на втому при контактній деформації:
- перевірочний розрахунок
![]() ,
(4.34)
,
(4.34)
де ![]() - безрозмірний
коефіцієнт, який враховує форму спряжених поверхонь зубців;
- безрозмірний
коефіцієнт, який враховує форму спряжених поверхонь зубців; ![]() - коефіцієнт, який враховує механічні
властивості матеріалів зубчастих коліс;
- коефіцієнт, який враховує механічні
властивості матеріалів зубчастих коліс; ![]() -
коефіцієнт сумарної довжини контактних ліній спряжених зубців, визначається:
для прямозубих передач
-
коефіцієнт сумарної довжини контактних ліній спряжених зубців, визначається:
для прямозубих передач ![]() ;
для косозубих і шевронних передач
;
для косозубих і шевронних передач ![]() . Тут
. Тут ![]() - коефіцієнт торцевого перекриття;
- коефіцієнт торцевого перекриття; ![]() - коефіцієнт навантаження,
визначається
- коефіцієнт навантаження,
визначається ![]() ,
де
,
де ![]() - коефіцієнт
розподілу навантаження між зубцями;
- коефіцієнт
розподілу навантаження між зубцями; ![]() -
коефіцієнт розподілу навантаження по ширині вінця зубчастого колеса;
-
коефіцієнт розподілу навантаження по ширині вінця зубчастого колеса; ![]() - коефіцієнт динамічності
навантаження.
- коефіцієнт динамічності
навантаження.
- проектний розрахунок
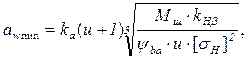 (4.35)
(4.35)
де ![]() - розрахунковий коефіцієнт,
приймається: для прямозубих передач
- розрахунковий коефіцієнт,
приймається: для прямозубих передач ![]() ;
для косозубих і шевронних передач
;
для косозубих і шевронних передач ![]() .
.
8. Прямозубі конічні передачі: основні геометричні співвідношення.

Зубчаста конічна передача – це трьохланковий
механізм у якого дві рухомі ланки є конічними зубчастими колесами (рис. 4.13).
Менше з двох зубчастих коліс 1 називається шестернею, а більше 2
– колесом. Термін “зубчасте колесо” належить до обох коліс передачі. Зубчасті
конічні передачі застосовують у тих випадках, коли осі валів перетинаються.
Коефіцієнт корисної дії їх рівний 0,95...0,96, оптимальне передаточне число ![]() .
.
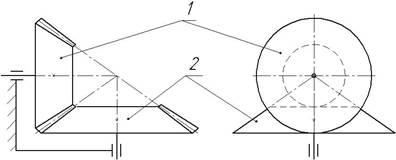
Рис.4.13. Схема зубчастої конічної передачі
Зубчасті конічні передачі класифікують за такими ознаками:
- за формою поперечного перетину зубців: евольвентні (рис. 4.14, а); циклоїдні (рис. 4.14, б); кругові (рис. 4.14, в);
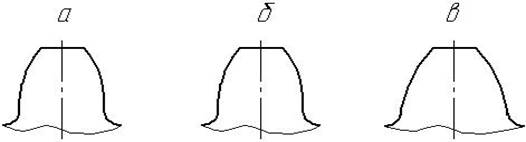
Рис. 4.14. Схеми форм поперечного перетину зуба
- за розміщенням на зубчастому вінці зубців:
- прямозубі (рис. 4.15, а);

- косозубі (рис. 4.15, б);

- кругові (рис. 4.15, в);

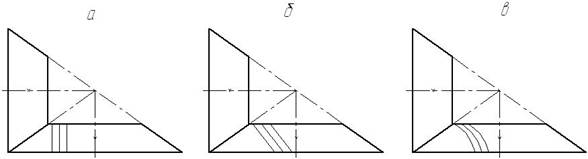
Рис.
4.15. Схеми розміщення зубців на зубчастому вінці
- за
кутом перетину осей ![]() :
:
з кутом ![]() (рис. 4.16, а);
(рис. 4.16, а);

з кутом ![]() (рис. 4.16, б);
(рис. 4.16, б);

з кутом ![]() (рис. 4.16, в);
(рис. 4.16, в);

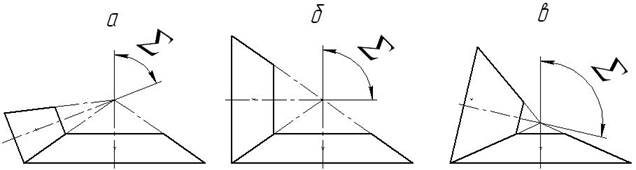
Рис. 4.16. Схеми за кутом перетину осей
- за конструкцією корпуса:
- відкриті (рис. 4.17, а);

- закриті (рис. 4.17, б).

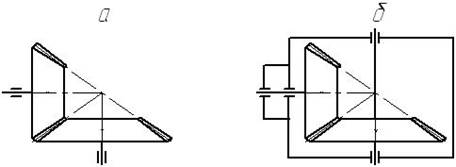
Рис. 4.17. Схеми передач за конструкцією корпуса
Питання про матеріали зубчастих конічних коліс, їх термообробку і виготовлення, види руйнування зубців і критерії їх роботоздатності, допустимі напруження розглядаються, як і для зубчастих циліндричних коліс.
Геометричні параметри і розміри.
Основний геометричний параметр зубчастої конічної
передачі є зовнішній коловий модуль ![]() -
число міліметрів зовнішнього ділильного діаметра (
-
число міліметрів зовнішнього ділильного діаметра (![]() ), що припадає на один зуб (
), що припадає на один зуб (![]() ). Крім того, зубчасті конічні
передачі мають середній коловий модуль
). Крім того, зубчасті конічні
передачі мають середній коловий модуль ![]() -
число міліметрів середнього ділильного діаметра (
-
число міліметрів середнього ділильного діаметра (![]() ), що припадає на один зуб (
), що припадає на один зуб (![]() ). Стандартним є зовнішній коловий модуль. Для визначення
геометричних розмірів зубчастої конічної передачі потрібно мати число зубців
шестерні (
). Стандартним є зовнішній коловий модуль. Для визначення
геометричних розмірів зубчастої конічної передачі потрібно мати число зубців
шестерні (![]() ) і число зубців
колеса (
) і число зубців
колеса (![]() ).
Рекомендується приймати
).
Рекомендується приймати ![]() ,
а
,
а ![]() , де
, де ![]() - передаточне число зубчастої
конічної передачі.
- передаточне число зубчастої
конічної передачі.
Для передач стандартного вихідного контуру по СТ СЭВ 516-77 (який встановлює кут профіля зуба α = 20°, коефіцієнт висоти головки зуба ha*=1,0 і коефіцієнт радіального зазору c* = 0,2) розміри зубчатої передачі визначаються за формулами.
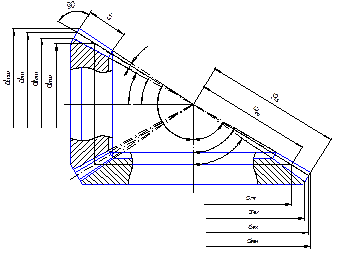
Рис. 4.18 Геометричні розміри конічної зубчастої передачі
Зовнішня ділильна конусна відстань ![]() .
(4.36)
.
(4.36)
Ширина
вінця зубчастих
коліс
![]() .
(4.37)
.
(4.37)
Середня
ділильна конусна відстань ![]() .
(4.38)
.
(4.38)
Середній коловий
модуль
![]() .
(4.39)
.
(4.39)
Зовнішня висота головки
зуба
![]() .
(4.40)
.
(4.40)
Зовнішня висота ніжки
зуба
![]() .
(4.41)
.
(4.41)
Зовнішня висота
зуба
![]() .
(4.42)
.
(4.42)
Кут
головки
зуба
![]() .
(4.43)
.
(4.43)
Кут
ніжки зуба
![]() .
(4.44)
.
(4.44)
Розміри шестерні:
- зовнішній
ділильний
діаметр
![]() ;
;
- середній
ділильний
діаметр
![]() ;
;
- кут
ділильного
конуса
![]() ;
;
- зовнішній
діаметр вершин
зубів
![]() ;
(4.45)
;
(4.45)
- зовнішній
діаметр
западин
![]() ;
;
- кут
конуса вершин
![]() ;
;
- кут
конуса
западин
![]() .
.
Розміри колеса:
- зовнішній
ділильний
діаметр
![]() ;
;
- середній
ділильний
діаметр
![]() ;
;
- кут
ділильного
конуса
![]() ;
;
- зовнішній
діаметр вершин
зубів
![]() ;
(4.46)
;
(4.46)
- зовнішній
діаметр западин
![]() ;
;
- кут
конуса
вершин
![]() ;
;
- кут
конуса
западин
![]() .
.
Тут ![]() -
коефіцієнт ширини зубчастого вінця.
-
коефіцієнт ширини зубчастого вінця.
2. Сили в зачепленні.
У зубчастих конічних передачах діють колові, радіальні та осьові сили.
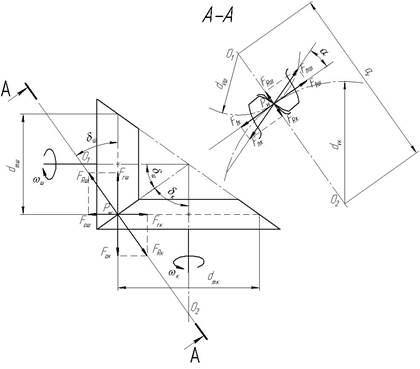
Рис. 4.19. Схема сил у зачепленні
Для зачеплення прямозубої конічної передачі виконуються
рівності: ![]() ;
; ![]() ;
; ![]() , де
, де ![]() і
і ![]() ,
, ![]() і
і ![]() ,
, ![]() і
і ![]() - сили в зачепленні, відповідно
колові, радіальні
та осьові на шестерні і колесі, які
визначаються:
- сили в зачепленні, відповідно
колові, радіальні
та осьові на шестерні і колесі, які
визначаються:
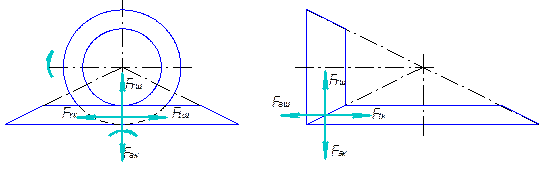
Рис. 4.20. Схема сил в передачі
- для шестерні ![]() ;
;![]() ;
;![]() ; (4.47)
; (4.47)
-
для колеса ![]() ;
; ![]() ;
; ![]() .
(4.48)
.
(4.48)
10. Особливості розрахунку, конструкція зубчастих коліс.
Для розрахунку зубців конічних передач на втому
при згині заміняємо зуб конічного зубчастого колеса (рис. 4.21, а) на
еквівалентний зуб циліндричного зубчастого колеса з середнім перетином
(рис.4.21,б), розміри якого визначаються через середній модуль ![]() .
.
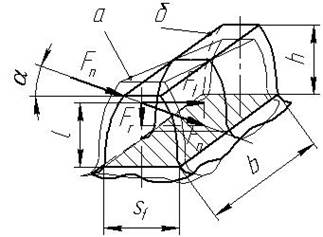
Рис. 4.21. Розрахункова схема зуба на згин
Тому подібно до зубчастої циліндричної передачі можна отримати формули для розрахунку зубчастих конічних передач на втому при згині.
Для перевірочного розрахунку:
![]() (4.49)
(4.49)
де ![]() - коефіцієнт форми зуба, вибирається
за еквівалентним числом зубців шестерні (
- коефіцієнт форми зуба, вибирається
за еквівалентним числом зубців шестерні (![]() ) і колеса (
) і колеса (![]() ):для прямозубих передач
):для прямозубих передач ![]() і
і ![]() ;
; ![]() - коефіцієнт перекриття зубців,
приймається;
- коефіцієнт перекриття зубців,
приймається; ![]() -
коефіцієнт нахилу зубі;
-
коефіцієнт нахилу зубі; ![]() -
коефіцієнт навантаження при згині, визначається за формулою
-
коефіцієнт навантаження при згині, визначається за формулою ![]() , де
, де ![]() - коефіцієнт розподілу навантаження
між зубцями;
- коефіцієнт розподілу навантаження
між зубцями; ![]() -
коефіцієнт розподілу навантаження по ширині вінця зубчастого колеса;
-
коефіцієнт розподілу навантаження по ширині вінця зубчастого колеса; ![]() - коефіцієнт динамічності
навантаження. Розрахунок на втому при згині виконується для зубців шестерні і
колеса.
- коефіцієнт динамічності
навантаження. Розрахунок на втому при згині виконується для зубців шестерні і
колеса.
Для проектного розрахунку:
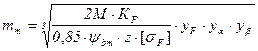 ,
(4.50)
,
(4.50)
де ![]() -
коефіцієнт ширини зубчастого вінця.
-
коефіцієнт ширини зубчастого вінця.
Щоб забезпечувати потрібну міцність зубців при згині максимальним навантаженням, необхідно виконувати таку умову:
![]() .
(4.51)
.
(4.51)
Розрахункові формули перевірочних і проектних розрахунків зубців конічних передач на втому при контактній деформації можна отримати подібно до циліндричних передач. Для цього необхідно зубчасту конічну передачу замінити еквівалентною зубчастою циліндричною передачею, що показано на рис. 4.22.
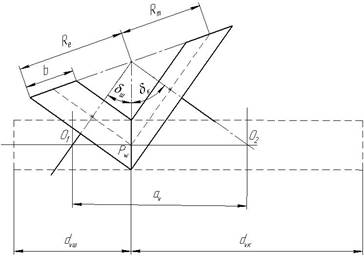
Рис. 4.22. Схема заміни конічної передачі еквівалентною циліндричною передачею
Для перевірочного розрахунку:
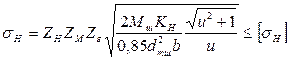 ,
(4.52)
,
(4.52)
де ![]() - безрозмірний коефіцієнт, який
враховує форму спряжених поверхонь зубців;
- безрозмірний коефіцієнт, який
враховує форму спряжених поверхонь зубців; ![]() -
коефіцієнт, який враховує механічні властивості матеріалів зубчастих коліс;
-
коефіцієнт, який враховує механічні властивості матеріалів зубчастих коліс; ![]() - коефіцієнт сумарної довжини
контактних ліній спряжених зубців, визначається: для прямозубих передач
- коефіцієнт сумарної довжини
контактних ліній спряжених зубців, визначається: для прямозубих передач ![]() .Тут
.Тут ![]() - коефіцієнт торцевого
перекриття;
- коефіцієнт торцевого
перекриття; ![]() -
коефіцієнт навантаження, визначається
-
коефіцієнт навантаження, визначається ![]() , де
, де ![]() - коефіцієнт розподілу навантаження
між зубцями;
- коефіцієнт розподілу навантаження
між зубцями; ![]() -
коефіцієнт розподілу навантаження по довжині зубців;
-
коефіцієнт розподілу навантаження по довжині зубців; ![]() - коефіцієнт динамічності
навантаження.
- коефіцієнт динамічності
навантаження.
Для проектного розрахунку:
![]() ,
(4.53)
,
(4.53)
де ![]() - розрахунковий коефіцієнт, для
прямозубої передачі
- розрахунковий коефіцієнт, для
прямозубої передачі ![]() .
.
Далі визначається зовнішній коловий модуль зубців
![]() ,
(4.54)
,
(4.54)
Значення зовнішнього колового модуля ![]() округляється
до стандартного і визначаються всі
геометричні розміри передачі.
округляється
до стандартного і визначаються всі
геометричні розміри передачі.
Щоб забезпечувати потрібну контактну міцність зубців при максимальному навантаженні, необхідно виконувати таку умову:
![]() .
(4.55)
.
(4.55)

Запитання для самоконтролю:
1. Назвіть призначення та будову зубчастих передач.
2. Як працюють зубчасті передачі ?
3. Вкажіть область застосування зубчастих передач.
4. За якими ознаками класифікують зубчасті передачі ?
5. Що називається коригуванням зубів та для чого воно застосовується ?
6. Якими методами виконують нарізання зубів ?
7. Яку обробку виконують після нарізання зубів ?
8. Назвіть матеріали, з яких виготовляють зубчасті колеса.
9. Назвіть види руйнування зубів.
10. Як визначити передаточне число для циліндричних зубчастих передач ?
11. Що називається модулем, які є модулі, який являється стандартним ?
12. Як визначаються діаметри вершин і западин зубів ?
13. Назвіть сили, що виникають у зачепленні прямозубої циліндричної передачі.
14. В чому заключається суть розрахунку зубчастих передач на контактну міцність зубів ?
15. З яких деталей складається зубчаста конічна передача ?
16. За якими ознаками класифікується зубчаста конічна передача ?
17. Назвіть основні геометричні параметри зубчастої конічної передачі.
18. Які сили виникають у зачепленні прямозубої конічної передачі ?
19. В чому заключається суть розрахунку конічних прямозубих передач на контактну міцність зубів ?
20. В чому заключається суть розрахунку конічних прямозубих передач на міцність зубів при згині ?