Процеси і апарати харчових виробництв Електронний підручник
Головна Теоретичні відомості Лабораторні та практичні роботи Тести Додатки Список використаних джерел	2.2 Основи термодинаміки
	1. Основні характеристики потоку та руху рідин. 2. Режим руху рідини в трубах. Критерії Рейнольдса. 3. Рівняння Бернуллі для ідеальної та реальної рідини. 1. Основні характеристики потоку та руху рідин Гідродинаміка вивчає закони руху рідин під дією зовнішніх сил. У гідродинаміці рідина є суцільним середовищем, частки якого наближено можна розглядати як окремі матеріальні точки. Як і в гідростатиці, в гідродинаміці користуються поняттям ідеальної рідини. Даними, здобутими для ідеальної рідини, користуються на практиці з доповненням необхідними поправками на властивості самої рідний. Рух рідини характеризується швидкістю руху окремих часток та гідродинамічним тиском. У загальному випадку для потоку рідини швидкість U руху окремих часток і гідродинамічний тиск р є функцією координат точок простору і часу: , . Рух рідини може бути усталеним неусталеним, рівномірним і нерівномірним, напірним і безнапірним. Усталеним називають рух, коли через фіксовану в просторі точку проходять окремі частки рідини в різні проміжки часу з однаковими швидкістю і тиском: U = тобто швидкість U і тиск є тільки функціями координат точок простору. Прикладом може бути перекачування рідини відцентровими насосами або витікання рідини з отвору при сталому напорі. Неусталеним називають рух, коли через фіксовану в просторі точку проходять окремі частки рідини в різні проміжки часу з різними швидкістю U і тиском р: , , тобто швидкість і тиск е функціями координат точок простору і часу. Прикладом може бути перекачування рідини поршневими насосами без установки повітряних ковпаків або витікання рідини з отвору при змінному напорі. Рис.1. Рівномірним усталеним називають рух, коли гідравлічні характеристики окремих часток не змінюються вздовж потоку. Прикладом може бути ламінарний рух у круглій трубі зі сталою площею перерізу. До нерівномірного усталеного можна віднести рух, коли гідравлічні характеристики окремих часток уздовж потоку не залишаються сталими. Прикладом може бути течія рідини в тих місцях, де є раптове розширення чи звуження потоку. Місцевою швидкістю вважають миттєву швидкість окремої частки рідини в довільній точці потоку. 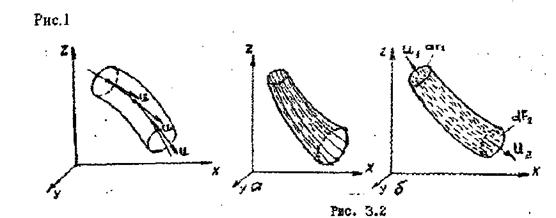При усталеному русі ця швидкість є функцією координат точок простору U = , а при неусталеному - функцією точок координат і часу U = Лінією течії вважають таку лінію, дотичні до якої збігаються з напрямом векторів швидкостей точок, які в цю мить на ній перебувають (рис.2) Лінію течії для усталеного руху можна уявити як траєкторію окремих часток. Трубчасту замкнену поверхню, яка створена лініями течії, називають трубкою течії (рис.2,а). Рис.2. Рис. 3. Лінії течії, які проходять всередині трубки течії, створюють елементарний струмок. Оскільки окремі частки рідини., які рухаються по лінії течії, не відриваються від неї, то поверхня трубки, створена лініями течії, непроникна для часток рідини ззовні і з середини трубки течії (рис. 3,б). Потік рідини - безмежна кількість елементарних струменів, які рухаються паралельно один одному. Переріз, перпендикулярний до напряму руху потоку рідини і зайнятий тільки нею, вважається живим перерізом потоку. Середньою вважають таку швидкість V, з якою мають рухатися окремі частки рідини через живий переріз, щоб забезпечити такі самі витрати як при дійсному розподілі швидкостей. 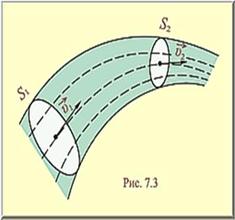Витрати - це об'ємна кількість рідини, яка проходить через живий переріз потоку за одиницю часу. Закон нерозривності потоку Виділимо в потоці рідини (рис.2.) елементарний струмінь з початковим перерізом dF1 і кінцевим dF2. У початковому перерізі швидкість U1, а в кінцевому - U2. При цьому в початковому перерізі витрати dQ1 =U1dF1, а в кінцевому - відповідно dQ2 =U2dF2. Оскільки поверхня трубки течії непроникна для часток рідини із сусідньої грубки, то можна зробити такий висновок: Рис.3. Рівняння нерозривності потоку Для потоку, який складається з безмежної кількості елементарних струменів, можна записати (1) де - середні швидкості. Вираз (1) називають законом нерозривності потоку, або заковом сталості витрат рідини. Якщо взяти два перерізи потоку, то , (2) тобто швидкості в потоці рідини розподіляються обернено пропорційно площі живих перерізів цього потоку. Рух рідини у трубопроводах може йти напірним і безнапірним. Напірним вважається рух, коли потік рідини повністю займає весь переріз труби, тобто коли частки рідини дотикаються до його стінок по всьому периметру. Якщо частки рідини дотикаються до стінок не по всьому периметру, тобто створюється вільна поверхня рідини в трубі, то такий рух - безнапірний. 2. Режим руху рідини в трубах. Критерії Рейнольдса Режими руху рідин. У кінці XIX ст. англійський фізик О. Рейнольдс проводив дослідження руху рідини в трубопроводах. 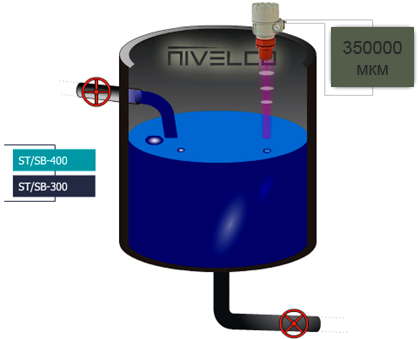За допомогою методу підфарбованих струменів Рейнольдс установив, що існує два режими течії рідини: ламінарний і турбулентний. На рис. 3 показано принципову схему досліду Рейнольдса. До посудини 1, у якій підтримується постійний рівень рідини, приєднано горизонтальну скляну трубу 2. У трубу 2 по її осі через капілярну трубку 6 із напірної ємності 4 вводиться тонка струминка тієї самої підфарбованої рідини. За невеликих швидкостей потоку в трубі 2 підфарбована струминка рухається, не змішуючись із основною масою рідини, у вигляді чітко вираженої тонкої нитки. Усі частинки рідини рухаються паралельно й прямолінійно. 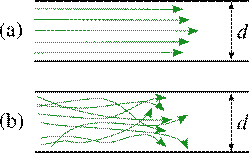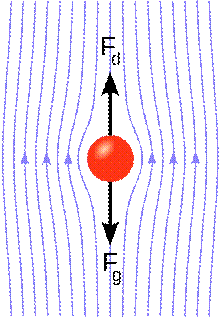Такий рух називається ламінарним (від латинського слова lamina (смужка, пластина). Рис.4. Схематичне зображення ламінарної (a) і турбулентної (b) течії в плоскому шарі Рис.5. Об'єкт, що рухається крізь газ або рідину зазнає дії сили в напрямку зворотному до його руху. Гранична швидкість досягається коли гальмівна сила стає рівною за величиною, але протилежною за напрямком до сили, що приводить тіло в рух. Показана куля в потоці з малим числом Рейнольдса. Рис. 6. Дослід Рейнольдса Якщо швидкість рідини в трубі 2 збільшувати, то з деякої межі підфарбована струминка набирає форми хвилястого руху, а потім починає розмиватися, змішуючись з основною масою рідини. Рух стає хаотичним, потік весь час перемішується, тому що окремі частинки рухаються за складними траєкторіями. Такий рух називається турбулентним (від латинського слова turbulentus - вихровий). Рейнольдс у своїх дослідах змінював не тільки швидкість, а й діаметр трубопроводу та в'язкість рідин шляхом їх підігріву, охолодження або заміни. При цьому він установив, що режим руху рідини повністю визначається безрозмірним комплексом: Re =vdρ/ = vd/v, (10) де v - середня швидкість потоку, м/с; d - діаметр трубопроводу, м; ρ - густина потоку, кг/м^3; - динамічний коефіцієнт в'язкості рідини, Па с; v - кінематичний коефіцієнт в'язкості, м^2/с. Цей комплекс називають по імені його автора критерієм, або числом, Рейнольдcа. Дослідом установлено, що зміна режимів течії рідини в циліндричних трубах відбувається при Reкр= 2320. У промислових і природних умовах найбільше поширений турбулентний режим руху. 3. Рівняння Бернуллі для ідеальної та реальної рідини Рівняння Бернуллі для ідеальної та реальної рідини. Рівняння Бернуллі встановлює зв'язок між швидкістю потоку рідини в трубопроводі і тиском у потоці рідини. Первісно рівняння було одержано для ідеальної рідини. В потоці ідеальної рідини потенційна енергія, яка створюється насосом, перетворюється на кінетичну енергію потоку. Перетворення енергії відбувається без витрат, тому що в ідеальній рідині немає витрат на подолання сил тертя. Тому повна питома енергія потоку постійна в будь-якому його перерізі. 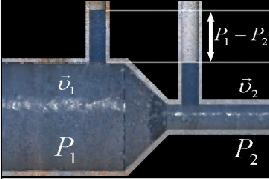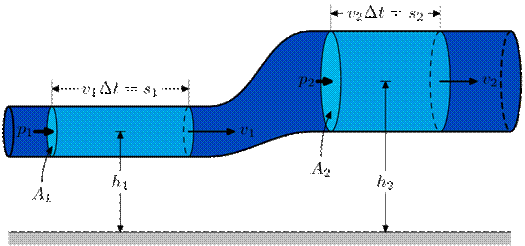Рис.7. Пояснення рівняння Бернуллі Основне рівняння гідростатики (5) стверджує постійність величини питомої потенційної енергії нерухомого об'єму ідеальної рідини в двох точках, тобто Тепер уявимо собі, що розглянутий нами об'єм ідеальної рідини рухається зі швидкістю v. Тоді, крім потенційної енергії, він володітиме також кінетичною енергією, яка визначається виразом v^2 / (2g). Умова збереження енергії потоку може бути записана - як сума трьох напорів: z + p / (ρg) + v^2/ (2g) = const. (11) Перший член рівняння (11) визначає геометричну висоту, або геометричний напір, другий - питому потенційну енергію тиску, третій - питому кінетичну енергію, або швидкісний напір. Для двох перерізів потоку ідеальної рідини рівняння (11) запишеться так: z1 + p1 / (ρg) + v/ (2g) = z2 + p2 /(ρg) + v /(2g). (12) Це і є рівняння питомої енергії ідеальної рідини, яка рухається (рівняння Бернуллі). Під час руху реальної рідини мають місце втрати енергії на подолання сил внутрішнього тертя між частинками рідини й зовнішнього тертя між частинками рідини та стінками труби. Мають місце також втрати енергії на подолання місцевих опорів. Тому для збереження балансу енергії під час руху реальної рідини права частина рівняння Бернуллі доповнюється величиною втраченого напору h1-2 на подолання сил тертя рідини об стінки труби і внутрішнє тертя, при її переміщенні з перерізу 1 у переріз 2: z1 + p1 / (ρg) + v/ (2g) = z2 + p2 /(ρg) + v /(2g) + h1-2 (13) Контрольні запитання 1. Назвіть приклад усталеного руху рідини. 2. Запишіть рівняння нерозривності потоку. 3. Який режим руху рідини називається ламінарним? 4. Який режим руху рідини називається турбулентним? 5. Що таке критичне значення числа Рейнольдса? 6. Запишіть рівняння Бернуллі для ідеальної і реальної рідини.
	Попередня тема	На початок	Наступна тема